Partição da unidade de alta regularidade para análise de estruturas
Partição da unidade de alta regularidade para análise de estruturas
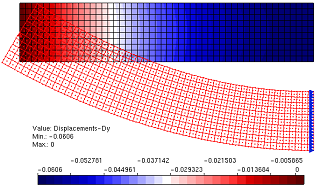
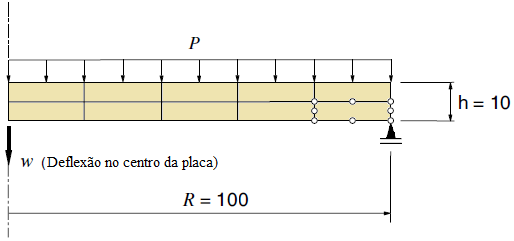
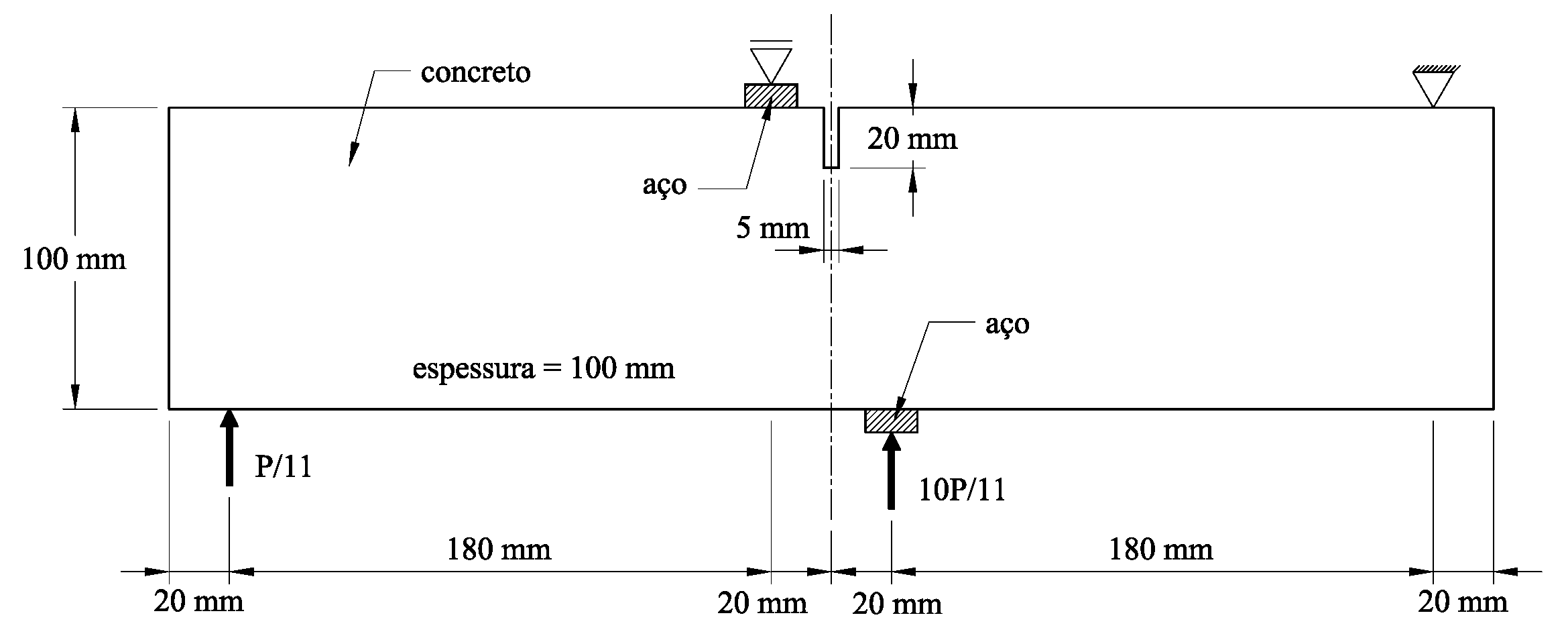
Em Duarte et al. (2006) e em Barros et al. (2007) as funções de PU do GFEM são construídas com base na mesma estratégia do Método das nuvens hp, possibilitando a obtenção de funções aproximadoras de continuidade do tipo Ck, onde k pode ser arbitrariamente definido. A partição da unidade de elevada regularidade foi implementada na plataforma computacional INSANE e seu desempenho foi avaliado em exemplos numéricos. Para validar os recursos implementados e exemplificar seu interesse, o problema da viga apresentado em Lee e Bathe (1993) é empregado. A Figura 1 apresenta esquematicamente a viga analisada. Com o objetivo de explorar as vantagens das funções de aproximação de elevada regularidade inseridas no INSANE neste trabalho, uma série de modelos do MEFG e do Método das Nuvens hp Ck com quatro células de integração e com diversos graus de aproximação foi analisada. Nas terceira, quarta e quinta colunas da Tabela 1 são mostrados os resultados destas análises em termos de deslocamento em y, energia de deformação e componente de tensão normal máxima, respectivamente. A segunda coluna indica o grau da aproximação empregada. Para os modelos do MEFG, o grau da aproximação p corresponde a um enriquecimento até o grau p-1. Para os modelos do Método das Nuvens hp, o grau da aproximação n corresponde a um enriquecimento até o grau p. O enriquecimento nestes casos significa multiplicar a PU em cada nó por uma base de monômios capaz de representar qualquer polinômio com grau menor ou igual a p-1 para o MEFG e p para o Método das Nuvens hp Ck A diferença de abordagem entre estes dois métodos está no fato de no primeiro a PU já ser linear. Sendo assim, para se obter uma aproximação de grau p, torna-se suficiente multiplicá-la por monômios de grau até p-1. Por outro lado, no Método das Nuvens hp Ck, a PU é racional e exige a multiplicação de monômios até a ordem p para se ter uma aproximação com esta característica. As aproximações do 2o grau, mostradas nas Figuras 2 e 3 apresentam soluções de qualidade semelhante no que diz respeito aos deslocamentos. Entretanto, as tensões no modelo do MEFG continuam descontínuas e inferiores às obtidas pelo Método das nuvens hp Ck. A continuidade das distribuições de tensão nos modelos com as funções Ck colocam em evidência a utilidade deste tipo de aproximação para análise não-linear física.
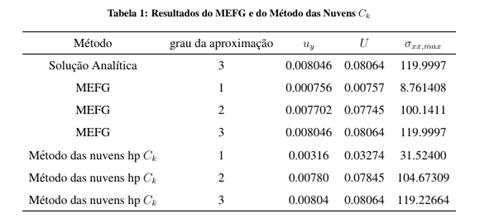
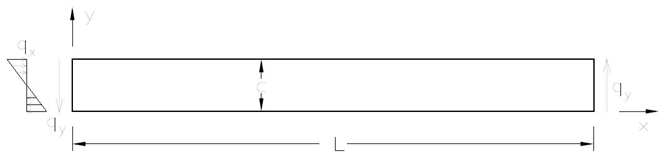
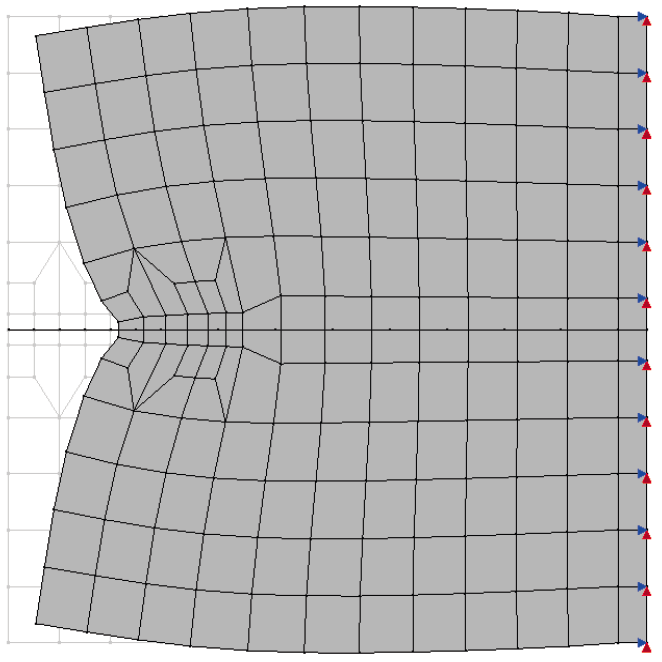
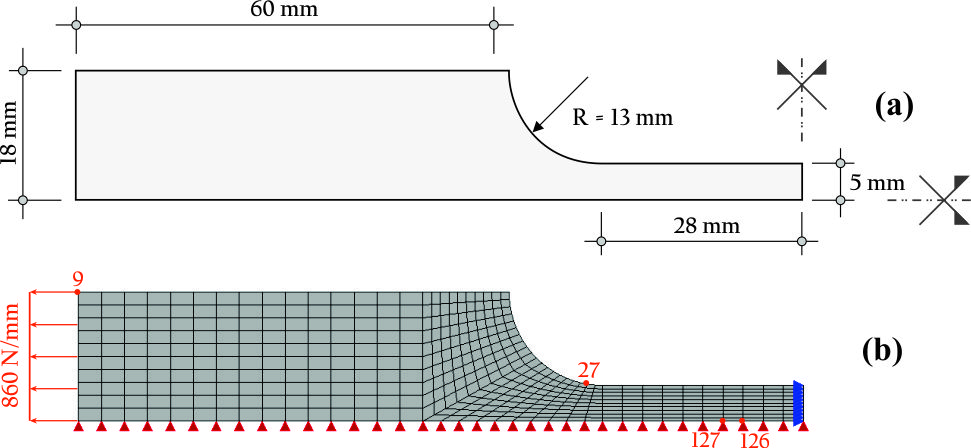
Figura 1 – Geometria

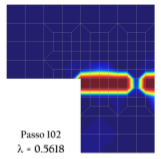
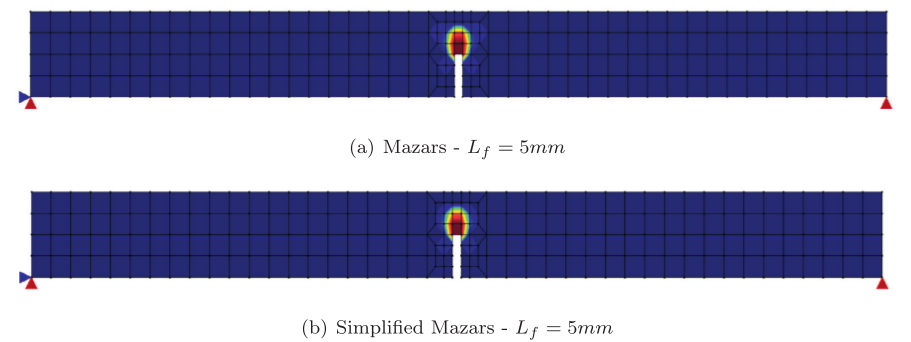
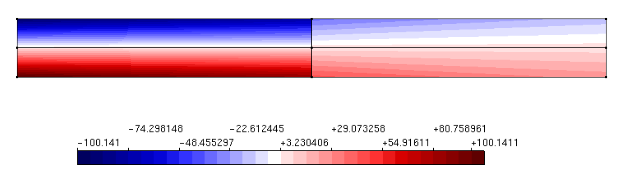
Figura 2 – MEFG – Componente de tensão normal na direção X – 4 células – Aproximação do 2º grau
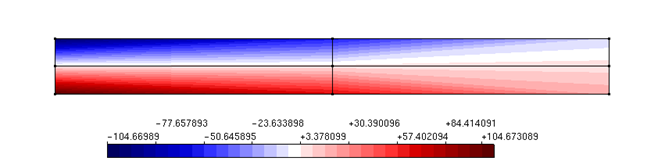
Figura 3 – Método das nuvens hp Ck – Componente de tensão normal na direção X – 4 Células – Enriquecimento do 2º grau
Referências
- Duarte, C. A., Kim, D.-J., & Quaresma, D. M., 2006. Arbitrarily smooth generalized finite element approximations. Computer Methods in Applied Mechanics and Engineering, vol. 196, pp. 33–56.
- Barros, F. B., de Barcellos, C. S., & Duarte, C. A., 2007. p-adaptive ck generalized finite element method for arbitrary polygonal clouds. Computational Mechanics, vol. 41, n. 1, pp. 175–187.
- Lee, N. S. & Bathe, K. J., 1993. Effects of element distortions on the performance of isoparametric elements. International Journal for Numerical Methods in Engineering, vol. 36, pp. 3553–3576.