High regularity Partition of Unity for structural analysis
High regularity Partition of Unity for structural analysis
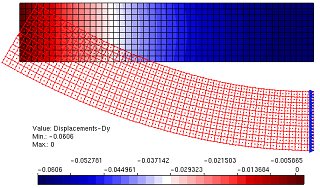
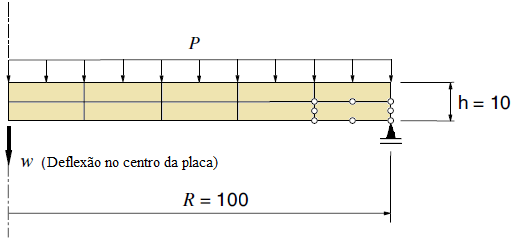
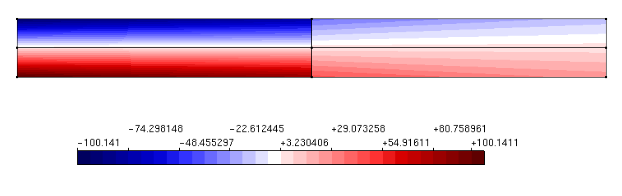
At Duarte et al. (2006) and Barros et al. (2007) the GFEM Partition of Unity is built based on the same strategy as the one employed at the hp-Cloud method. This strategy provides approximate functions of Ck continuity, with k arbitrarily defined. The high regularity Partition of Unity was implemented at the INSANE platform and its performance assessed by means of numerical simulations. To validate the implemented resources and bring its interest to evidence, a beam problem presented by Lee e Bathe (1993) is employed. The analyzed beam in presented at Fig. 1. Aiming to explore the advantages of the high regularity PoU added to the INSANE platform, a series of GFEM and hp-Clouds-Ck numerical models containing four integration cells and approximation functions of several degrees are presented. Results in terms of y axis displacement, strain energy and maximal normal stress are shown on the third, fourth and fifth columns of Table 1. The second column shows the model’s approximation degree. For the GFEM models, the approximate degree p indicates enrichment until the degree p-1. On the other hand, for the hp-Cloud method models, an approximate degree of p indicates enrichment until the degree p. The enrichment on those cases means that a product of the PoU on each node and a monomial base capable of representing any polynomial of degree minor or equal to p-1 to the GFEM and p to the hp-Cloud method is performed. This difference between the two approaches relies on the fact that the PoU is already linear at the GFEM method. Therefore, to obtain an approximate of degree p, the linear PoU should be multiplied by monomials until the degree p-1. On the other hand, because the PoU at the hp-Cloud-ck method is rational, the PoU should be multiplied by monomials until the degree p to obtain an approximation function with this character. According to the Figures 2 and 3, the second degree approximates of both kinds of models presents similar quality results as far as displacements are concern. Nevertheless, the stress diagram remains non-smooth and the stresses are lower than the ones obtained by the hp-Cloud-ck method. The continuity of the stress diagram of the hp-Cloud-Ck model brings to evidence the suitability of this kind of approximation to physical non linear analysis.
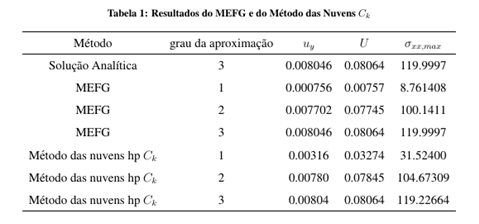
Figure 1 – Geometry

Figure 2 – GFEM – Normal stress component in X direction – 4 cells – 2nd degree approximation
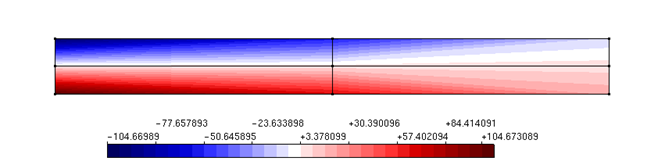
Figure 3 – hp-Cloud-ck – Normal stress component in X direction – 4 Cells – 2nd degree enrichment
References
- Duarte, C. A., Kim, D.-J., & Quaresma, D. M., 2006. Arbitrarily smooth generalized finite element approximations. Computer Methods in Applied Mechanics and Engineering, vol. 196, pp. 33–56.
- Barros, F. B., de Barcellos, C. S., & Duarte, C. A., 2007. p-adaptive ck generalized finite element method for arbitrary polygonal clouds. Computational Mechanics, vol. 41, n. 1, pp. 175–187.
- Lee, N. S. & Bathe, K. J., 1993. Effects of element distortions on the performance of isoparametric elements. International Journal for Numerical Methods in Engineering, vol. 36, pp. 3553–3576.