Imposição de condições de contorno em EFG via Método de Nitsche
Imposição de condições de contorno em EFG via Método de Nitsche
Diversos problemas analisados na Engenharia são descritos matematicamente por equações diferenciais que se tornam complexas ao buscar retratar com fidelidade o fenômeno analisado, bem como a complexidade da geometria. Os métodos numéricos, aliados à computação, são importantes ferramentas para a solução aproximada destes problemas. Dentre esses métodos destacam-se aqui o Método dos Elementos Finitos (MEF) e os Métodos sem Malha (MM).
O MEF é um método já consolidado, descrito por Moreira e Pitangueira (2006) como um método que pressupõe a divisão do domínio de estudo em subdomínios interconectados, denominados elementos finitos. Sua formulação é, geralmente, baseada nos deslocamentos quando aplicado na análise estrutural, ou seja, para cada um dos nós que formam os elementos, se tem uma função de interpolação para o cálculo de seus respectivos deslocamentos. É necessário estabelecer hipóteses relativas ao regime de deformações (relações deformações e deslocamentos), pequenas ou grandes deformações e ao comportamento do material (relações tensões e deformações). Essas três hipóteses são consideradas na obtenção das equações de equilíbrio nodais do elemento. Porém, esse método traz por definição uma dependência de malha, sendo que, ao discretizar o domínio em elementos, nota-se algumas dificuldades na análise de problemas com descontinuidade, grandes deformações ou gradientes elevados.
Os MM surgem como alternativa a essas dificuldades, pois esses métodos estabelecem uma discretização coerente entre a formulação das equações algébricas e os fenômenos de singularidade, em parte por não utilizarem uma malha pré-definida, mas também por descreverem os deslocamentos nodais de forma mais elaborada, capazes de captar variações mais abruptas nas grandezas nodais avaliadas. A discretização do domínio é feita apenas por pontos, conforme exposto por Liu (2009). Isso garante a independência de malha, uma das principais características do MM, que proporciona uma maior facilidade em tratar fenômenos como descontinuidade e fratura. Dentre os MM destacam-se os métodos: Element Free Galerkin (EFG), Reproducing kernel particle method (RKPM) Liu et al. (1995), Smoothed Particle Hydrodynamics (SPH) Monaghan (1992) e Meshless Local Petrov-Galerkin (MLPG) Atluri and Zhu (1998). Dentre esses métodos, destaca-se neste trabalho o EFG, método que apesar de não depender de malha para discretizar a geometria, necessita de células de integração, conhecidas como background cells, para realizar a integração no domínio.
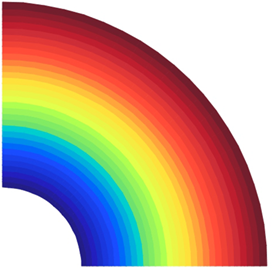
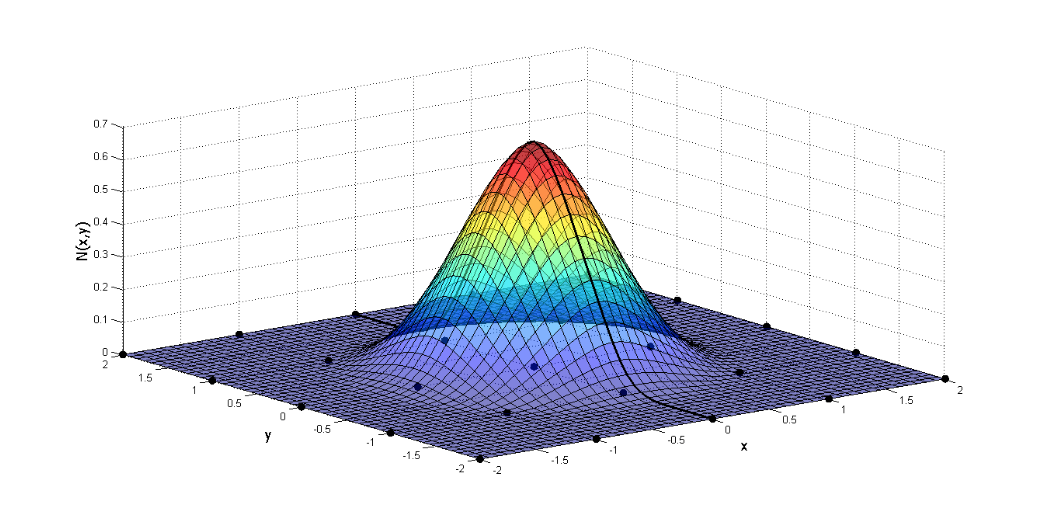
Apesar de tratarem-se de métodos robustos e eficientes, apresentam algumas desvantagens, em relação ao MEF. Segundo Silva (2012), por terem sua formulação baseada em funções de forma mais complexas, se comparada às do MEF que se restringem a funções de forma polinomiais, é necessária uma integração de maior ordem, aumentando assim o custo computacional. Tais funções de forma, em alguns MM, não apresentam a propriedade do Delta de Kronecker, como representado graficamente na Figura 1. Assim, a imposição das condições de contorno de Direchlet não é trivial, como no MEF.

Figura 1
Evidenciando a dificuldade na imposição das condições de contorno essenciais, segundo Fernandez-Mendez and Huerta (2003), pode-se dividir as técnicas para realizar a imposição em dois grupos. O primeiro é baseado em modificações da forma fraca, dentre as quais destacam-se: o Multiplicador de Lagrange (ML), o Método da Penalidade (MP) e o Método de Nitsche (MN). Já o segundo grupo caracteriza-se por métodos que estabelecem modificações das funções de forma, e traz como exemplo o acoplamento com elementos finitos. As diferentes formulações encontram-se na Figura 2.

Figura 2 – Equações 1, 2 e 3
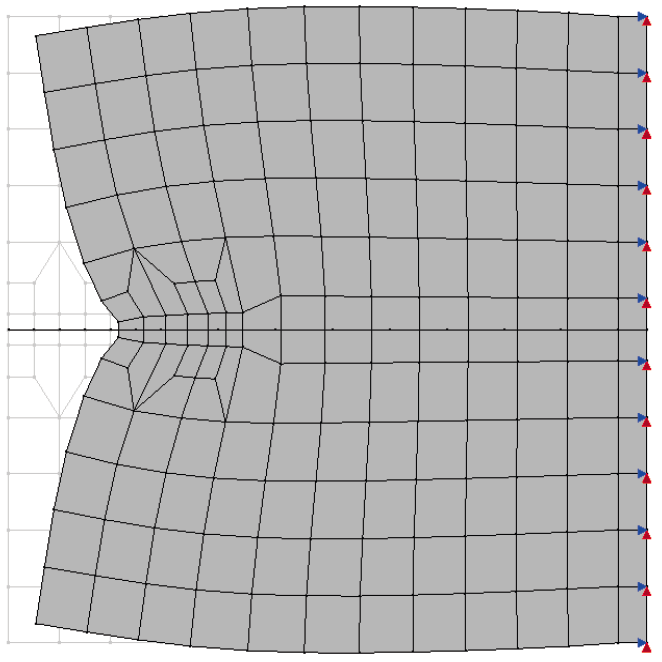
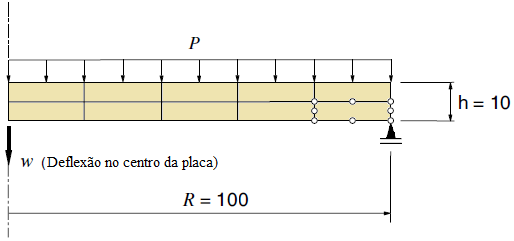
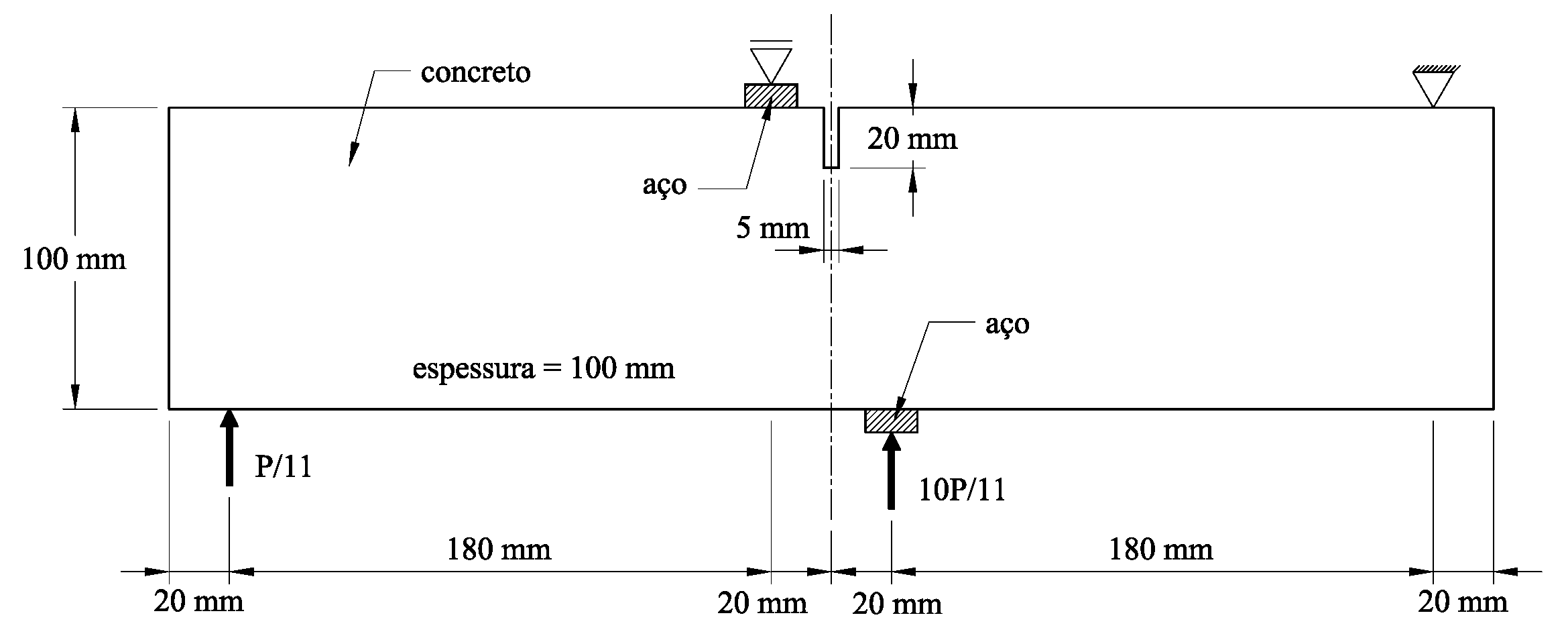
O objetivo desse trabalhado, realizado sob a orientação do Professor Ramon Silva, é implementar, no ambiente computacional INSANE, o Método de Nitsche como estratégia para a imposição de condição de contorno para o EFG, implementado por Silva (2012). Adicionalmente, comparar a acurácia dos resultados, contrapondo-os com aqueles obtidos utilizando as estratégias já implementadas no software e a solução exata, de um dos problemas abordados, que se encontra disponível na literatura. Baseando-se os estudos no trabalho de Augarde and Deeks (2008), discretizou-se inicialmente uma viga, de seção transversal retangular, em 85 nós regularmente distribuídos, com 4×16 células de integração (Figura 3).

Figura 3
O domínio de influência de cada nó é retangular de tamanho 5% maior que a distância entre os nós da discretização geométrica. O material utilizado, bem como a geometria do exemplo seguiu o que foi proposto no trabalho de Augarde and Deeks (2008), com módulo de elasticidade E = 1000 uf/ua, Poisson ν = 0.25 e dimensões de D = 2 uc, L = 8 uc e espessura unitária. Como I = D3/12, o momento de inércia de segunda ordem é 0.667 uc3. Aplicou-se na borda direita uma tensão com distribuição parabólica normal à direção Y, segundo a Equação 4. O modelo das análises é o Estado Plano de Tensão. Já como condição de vinculação, prescreveu-se o deslocamento analítico do problema conforme descrito nas Equações 5 e 6. Nessas equações, X e Y representam as coordenadas segundo o sistema cartesiano posicionado no centro da altura da viga e iniciando o eixo X na borda esquerda, conforme Figura 5. Para que essas condições de contorno naturais e essenciais fossem corretamente compreendidas no INSANE, foi necessário aplicar o carregamento equivalente à tensão descrita na Equação 4 como carga nodal com valor equivalente àquele obtido ao se integrar a área de influência de cada nó. Também se prescreveu como deslocamentos nodais os valores analíticos de deslocamento calculados nas Equações 5 e 6.
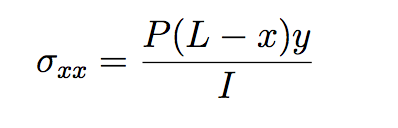
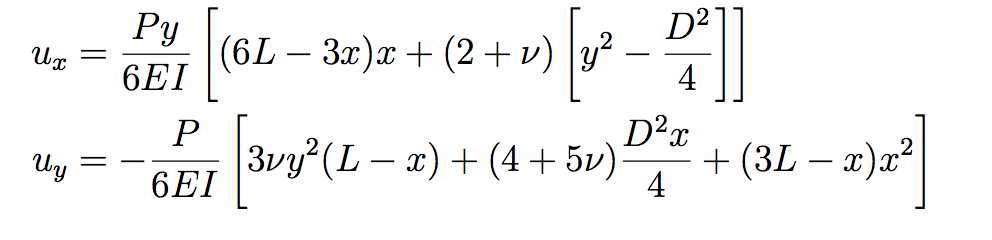 Figura 4 – Equações 4, 5 e 6
Figura 4 – Equações 4, 5 e 6

Figura 5
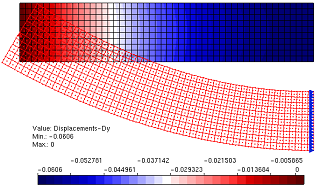
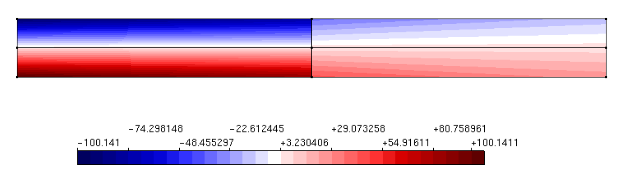
Comparação dos deslocamentos na direção Y obtidos com os diferentes métodos de imposição de contorno, Método da Penalidade, Multiplicadores de Lagrange e Método de Nietsche, bem como em comparação com os resultados via MEF. Em seguida o Gráfico 1 demonstra os valores comparativos ao resultado analítico nas diferentes discretizações, encontrados no contorno.
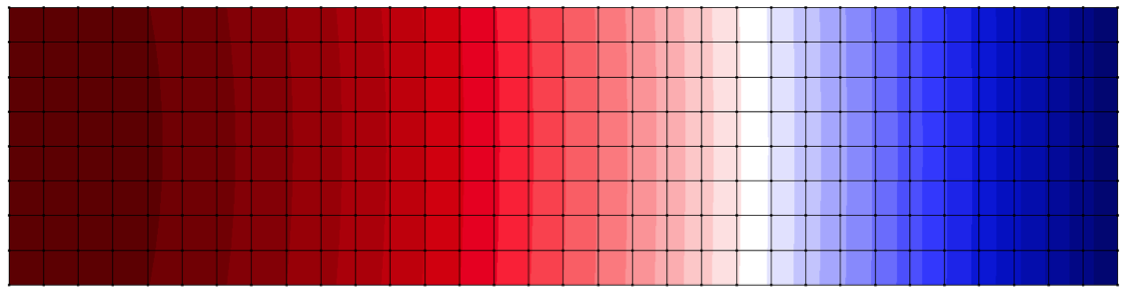
Figura 6 – Deslocamento na direção Y via MEF

Figura 7 – Deslocamento na direção Y via Multiplicadores de Lagrange

Figura 8 – Deslocamento na direção Y via Método da Penalidade β=1000

Figura 9 – Deslocamento na direção Y via Método de Nitsche β=1000
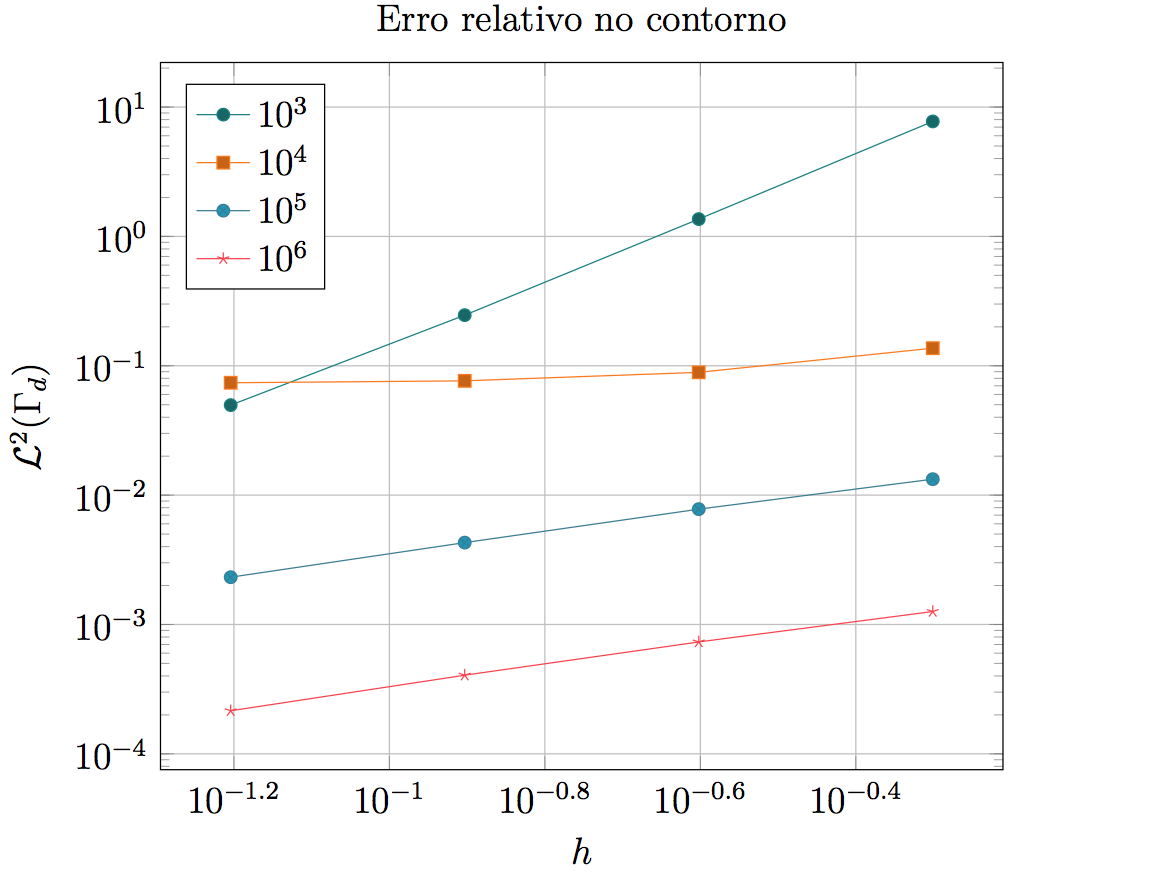
Gráfico 1
Pode-se observar, portanto, que o Método de Nitsche é capaz de impor as condições de contorno prescritas de forma satisfatória, tratando-se de um método que melhora sua aproximação com aumentos inferiores ao necessário para a aplicação da condição de contorno pelo Método da Penalidade. Ainda que sua precisão esteja fortemente relacionada com a ordem de grandeza do fator β, pode-se observar que foi necessário um valor inferior, para obter um menor erro nos deslocamentos calculados quando comparados aos deslocamentos obtidos de forma analítica, do que o necessário para que o método da penalidade satisfaça a mesma precisão.
Referências
- Atluri, S. N. and Zhu, T. (1998), ‘A new Meshless Local Petrov-Galerkin (MLPG) approach in computational mechanics’, Computational Mechanics 22(2), 117–127.
- Augarde, C. E. and Deeks, A. J. (2008), ‘The use of Timoshenko’s exact solution for a cantilever beam in adaptive analysis’, Finite Elements in Analysis and Design 44(9), 595–601.
- de Faria, B. R. L. (2013), Element Free Galerkin: Integração nodal conforme e estabilizada (SCNI) com método da penalidade e dos multiplicadores de lagrange, Master’s thesis, Universidade Federal de Minas Gerais.
- Fernandez-Mendez, S. and Huerta, A. (2003), ‘Imposing essential boundary conditions in mesh-free methods’, Elsevier Science .
- Moreira, R. N. and Pitangueira, R. L. (2006), ‘Aplicação gráfica interativa para ensino do método dos elementos finitos’.
- Silva, R. P. (2012), Análise fisicamente não linear com Método sem Malha, Tese de doutorado, Universidade Federal de Minas Gerais.