Simulação de nucleação e propagação de trincas usando GFEM

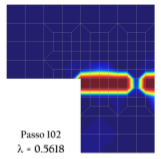
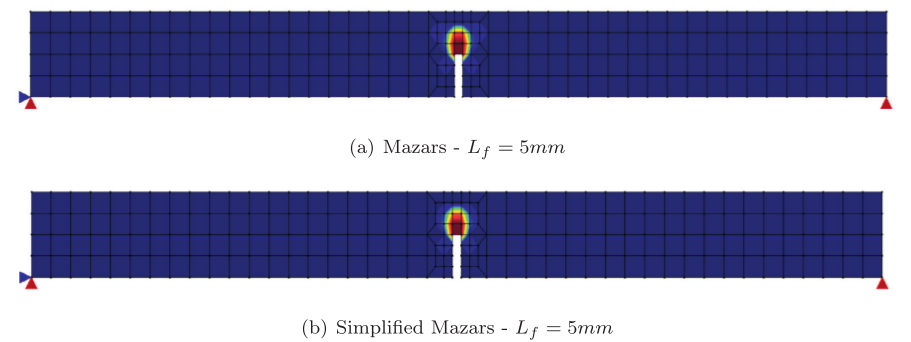
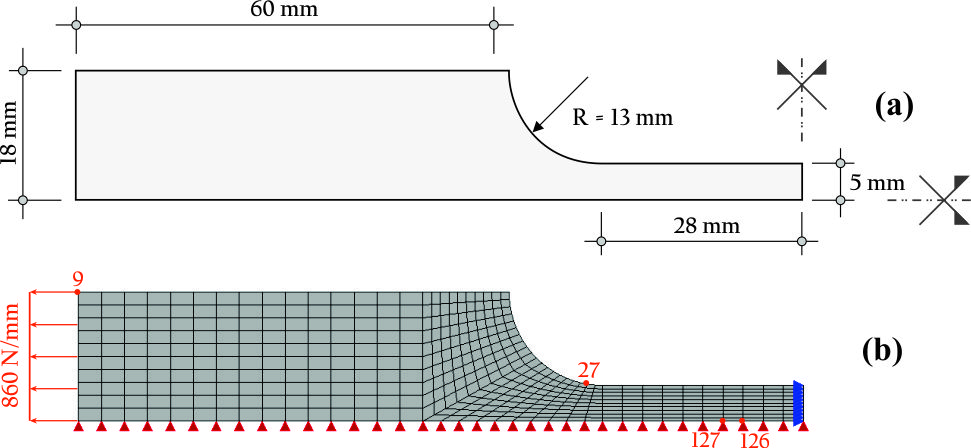
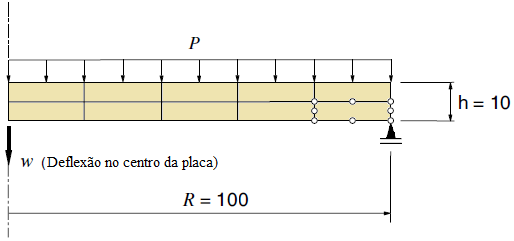
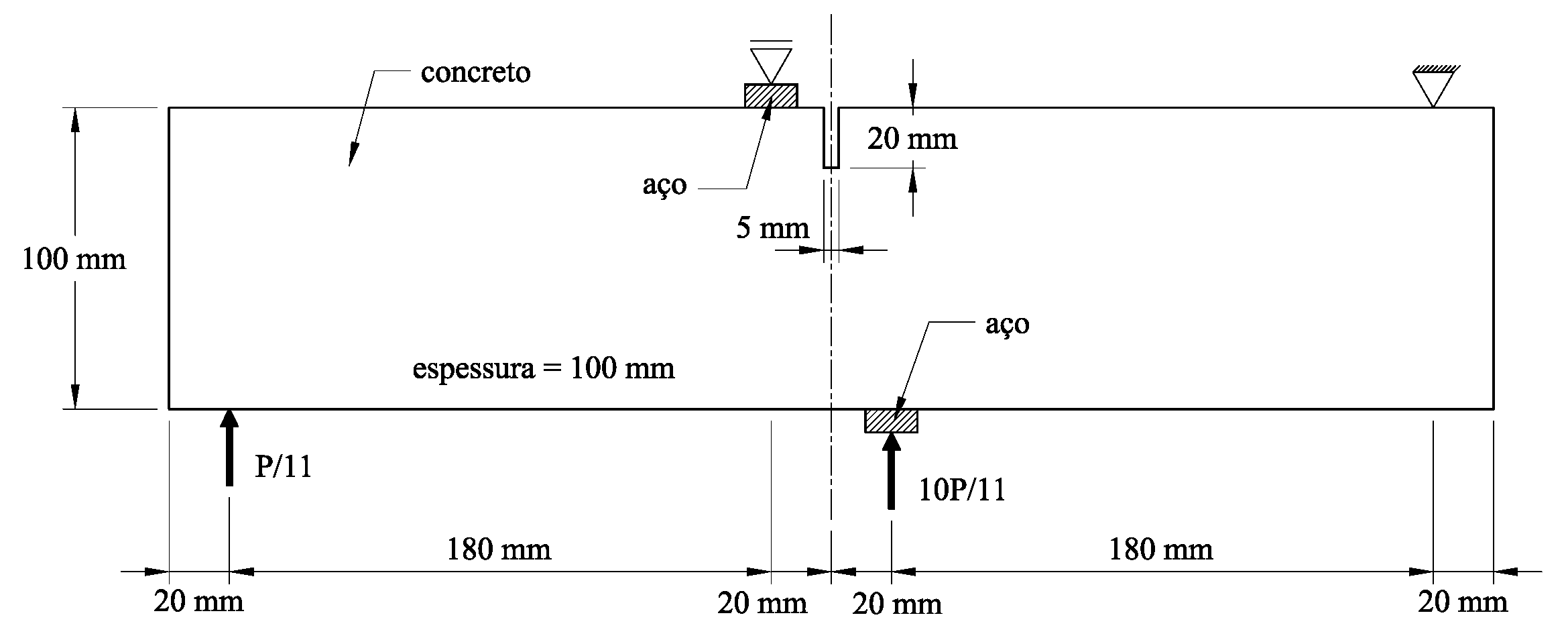
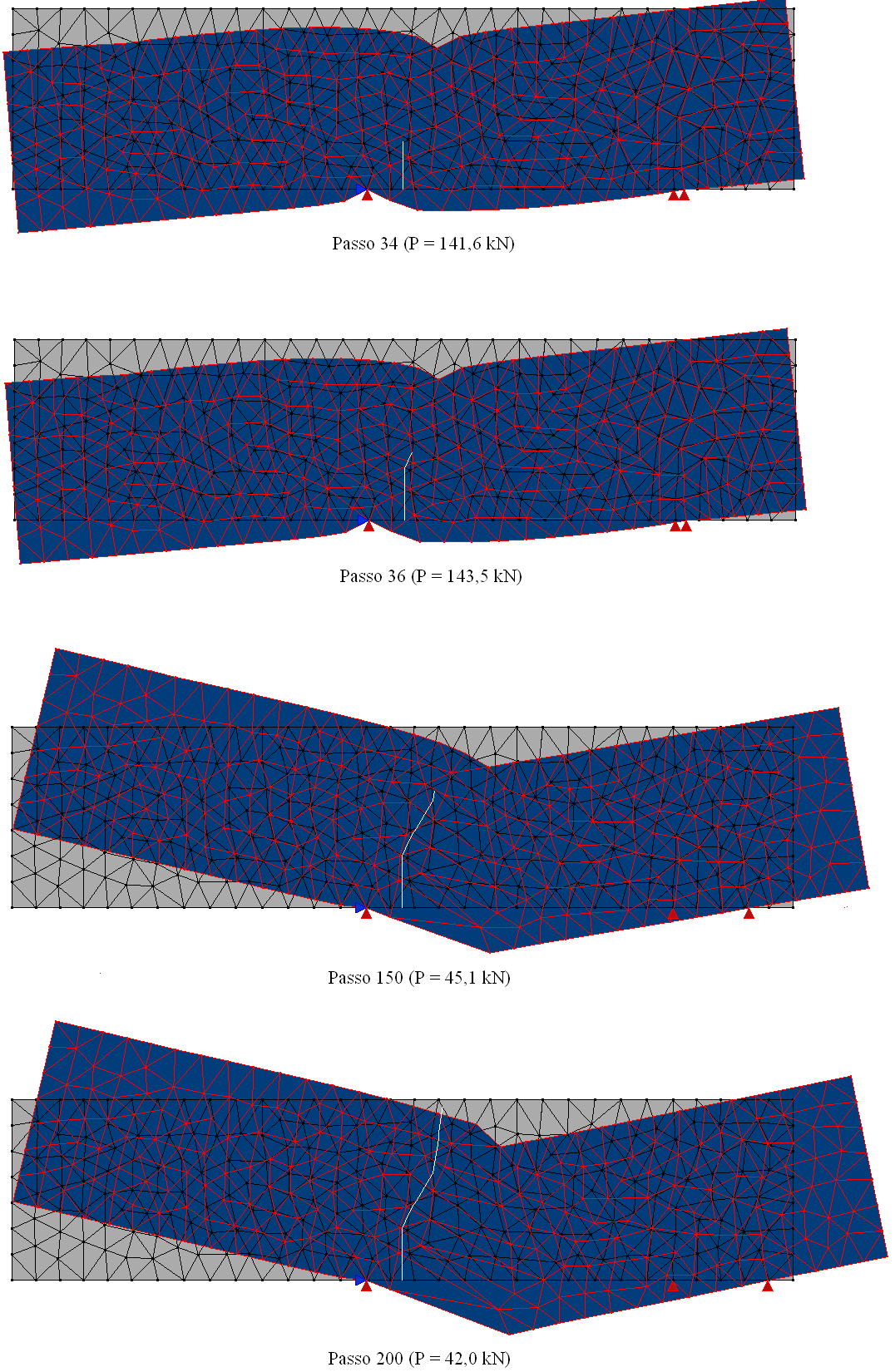
Visando reproduzir numericamente o ensaio de cisalhamento em 4 pontos realizado por Arrea e Ingraffea (1982), ilustrado na Figura 1, empregou-se o sistema INSANE, valendo-se do arcabouço teórico-computacional para simulação do processo de nucleação e propagação de trincas discretas, desenvolvido por Silva (2016). Na análise, adotou-se o modelo constitutivo de fissuras distribuídas com leis de Carreira e Chu (1985), para compressão, e Boone et al. (1986), para tração, cujos parâmetros do material são: E₀ = 24800,0 N/mm², ν = 0,18, f_c = 34,0 N/mm², f_t = 3,4 N/mm², ε_c = 0,002, G_f = 0,120 N/mm, h = 40 mm e β_r = 0,02. A viga foi modelada com elementos triangulares de três nós T3 em estado plano de tensão. A falha preexistente foi modelada como um entalhe, por meio de recurso disponibilizado no sistema encarregado de enriquecer os nós necessários para simulação do salto no campo de deslocamentos. Para solução do modelo, empregou-se o método de controle direto de deslocamento, incrementando-se de 0,00065 mm o grau de liberdade adicionado a um dos nós da aresta que contém a “boca” da trinca. Este grau de liberdade refere-se a uma parcela do deslizamento tangencial relativo desta “boca”, ou seja, controlou-se um quinhão do CMSD (Crack Mouth Sliding Displacement), com tolerância para convergência de 1 x 10^-3 e carga de referência P = 130000,0 N. Na Figura 2, apresenta-se a trajetória de equilíbrio do deslizamento tangencial relativo das extremidades da trinca (CMSD), comparando-a com os resultados experimentais de Arrea e Ingraffea (1982) e numéricos de Fang et al. (2008), que por sua vez analisaram a viga com um modelo constitutivo de trinca coesiva que adota leis exponencial e bilinear, em um modelo de elementos finitos estendidos. Nas Figuras 3 e 4, apresentam-se, respectivamente, a deformada com fator de escala igual a 500 e a tensão de cisalhamento τ_xy ao longo do domínio, para os passos 34 (141,6 kN), 36 (143,5 kN), 150 (45,1 kN) e 200 (42,0 kN).

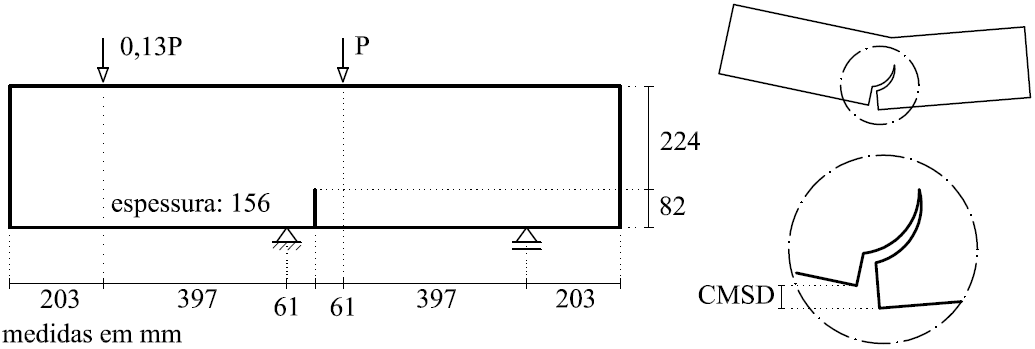
Figura 1 – Geometria

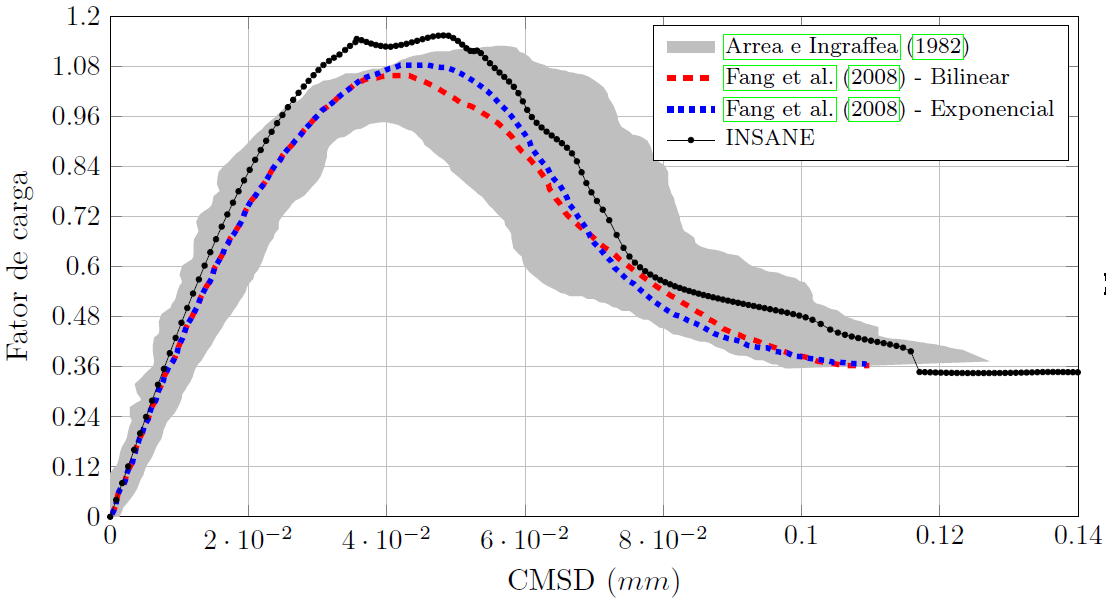
Figura 2 – Curvas CMSD x fator de carga

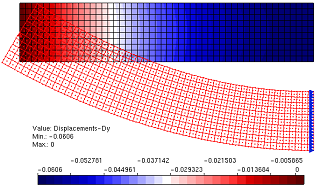
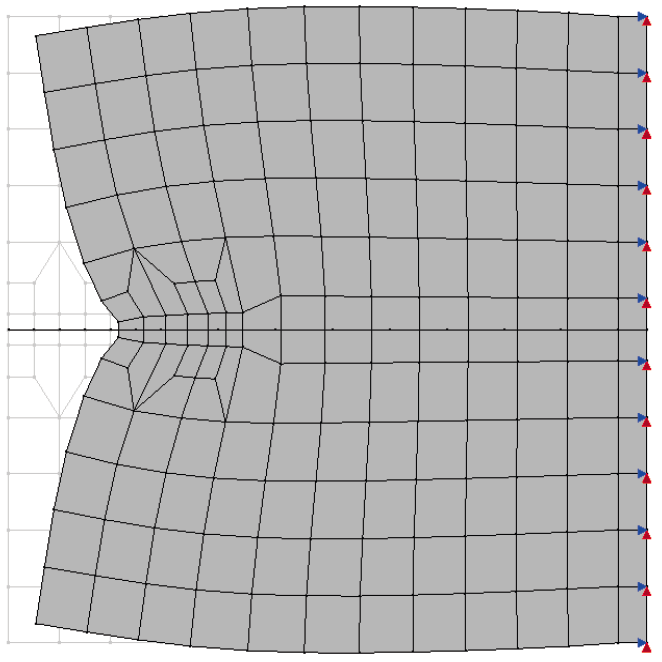
Figura 3 – Deformada

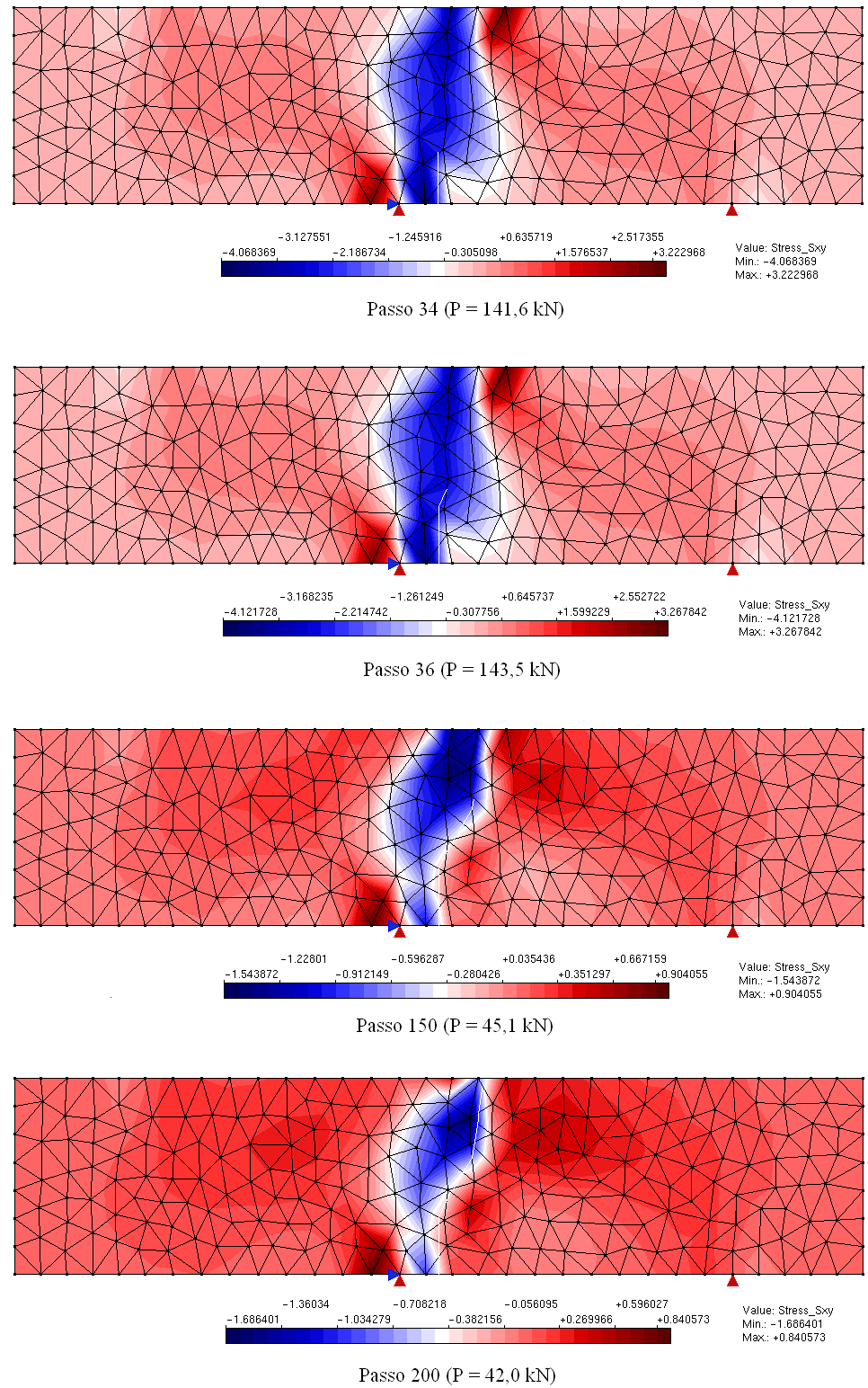
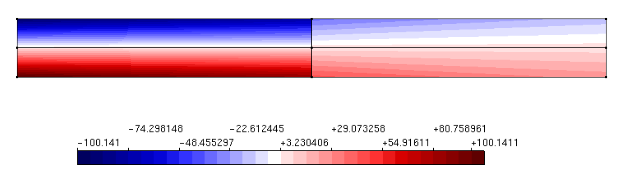
Figura 4 – Tensão de cisalhamento τxy

Referências

• Arrea, M. e Ingraffea, A., 1982. Mixed mode crack propagation in mortar and concrete. Relatório técnico 81-13, Departement of Structural Engineering, Cornell University, Ithaca, EUA. Citado por Rots et al. (1985).
• Boone, T., Wawrzynek, P. A. e Ingraffea, A. R., 1986. ‘Simulation of the fracture process in rock with application to hydrofracturing’. International Journal of Rock Mechanics and Minig Science, vol. 23 (3), pp. 255-265.
• Carreira, D. J. e Chu, K., 1985. ‘Stress-strain relationship for plain concrete in compression’. ACI Journal, vol. 82, pp. 797-804.
• Fang, X.-J., Jin, F. e Yang, Q.-D., 2008. ‘Extended finite-element analysis of fractures in concrete’. Engineering and Computational Mechanics, vol. 161, pp. 187-197.
• Rots, J. G., Nauta, P., Kusters, G. M. e Blaauwendrra, J., 1985. ‘Smeared crack approach and fracture localization in concrete’. HERON 30, vol. (1), pp. 1-48.
• Silva, L. L., 2016. Sistema gráfico interativo para análise de nucleação e propagação de trincas. Dissertação de mestrado, Universidade Federal de Minas Gerais, Belo Horizonte, MG, Brasil.