G/XFEM – Modelo de fissura coesiva

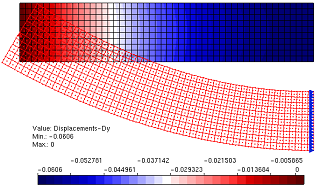
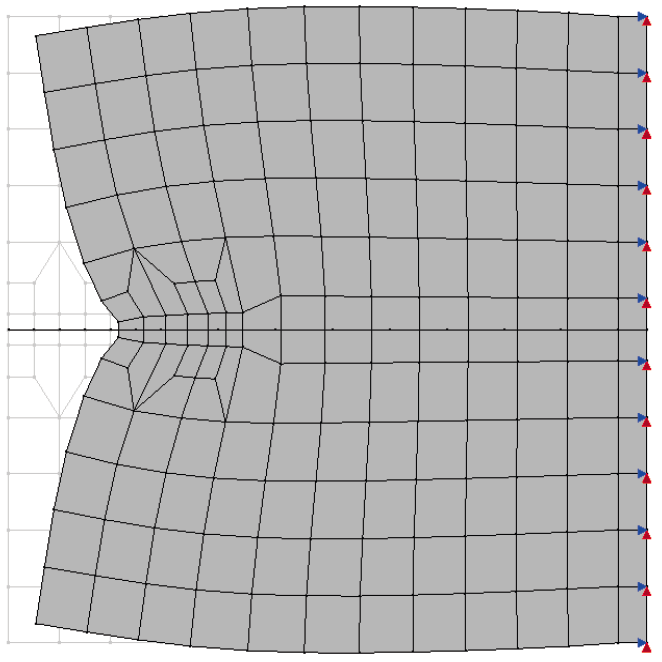
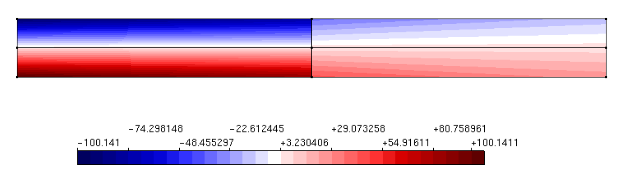
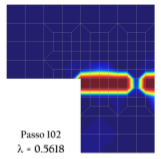
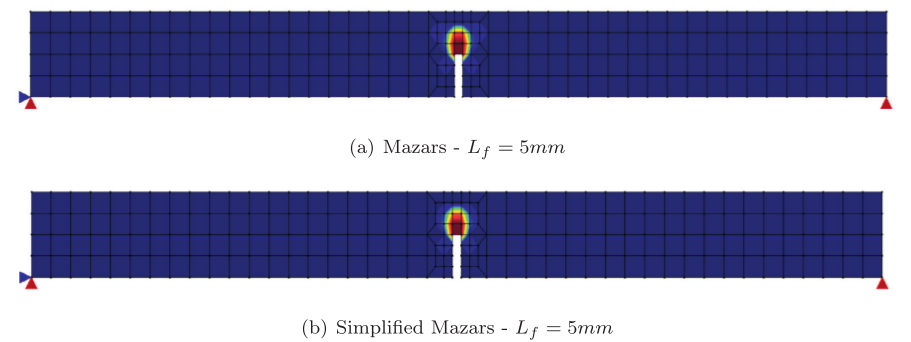
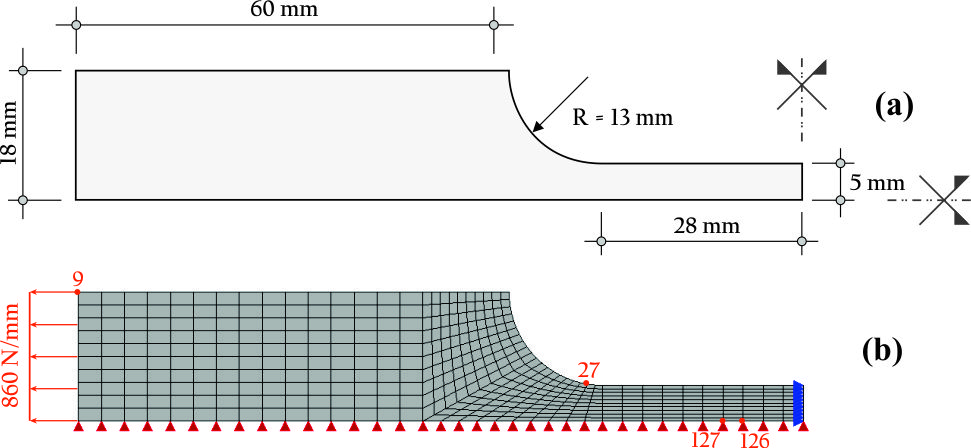
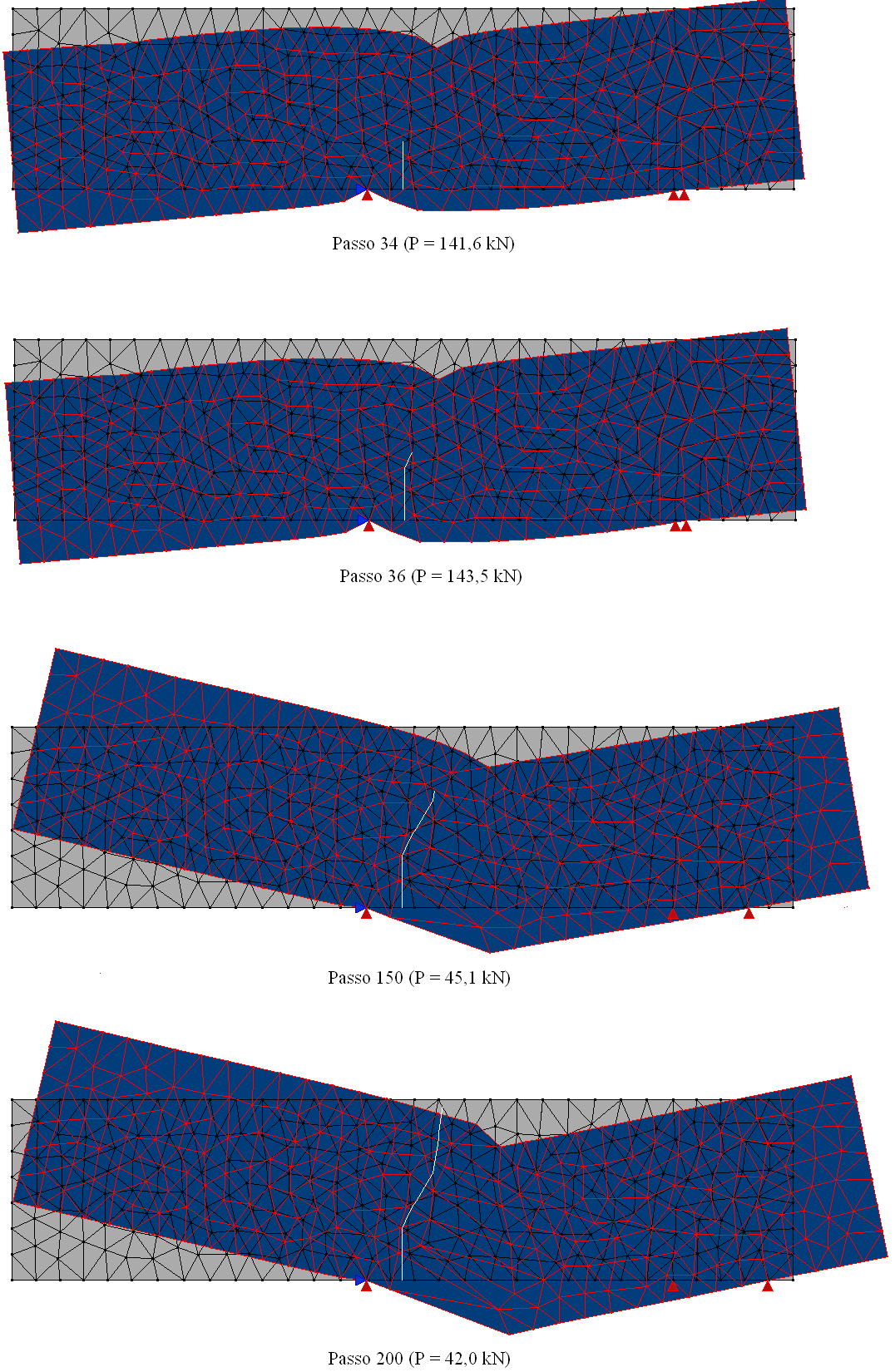
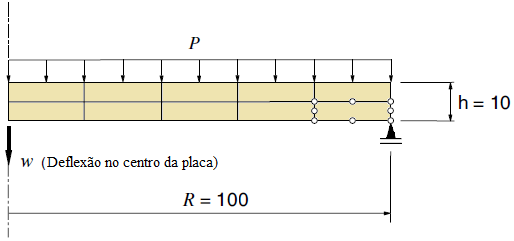
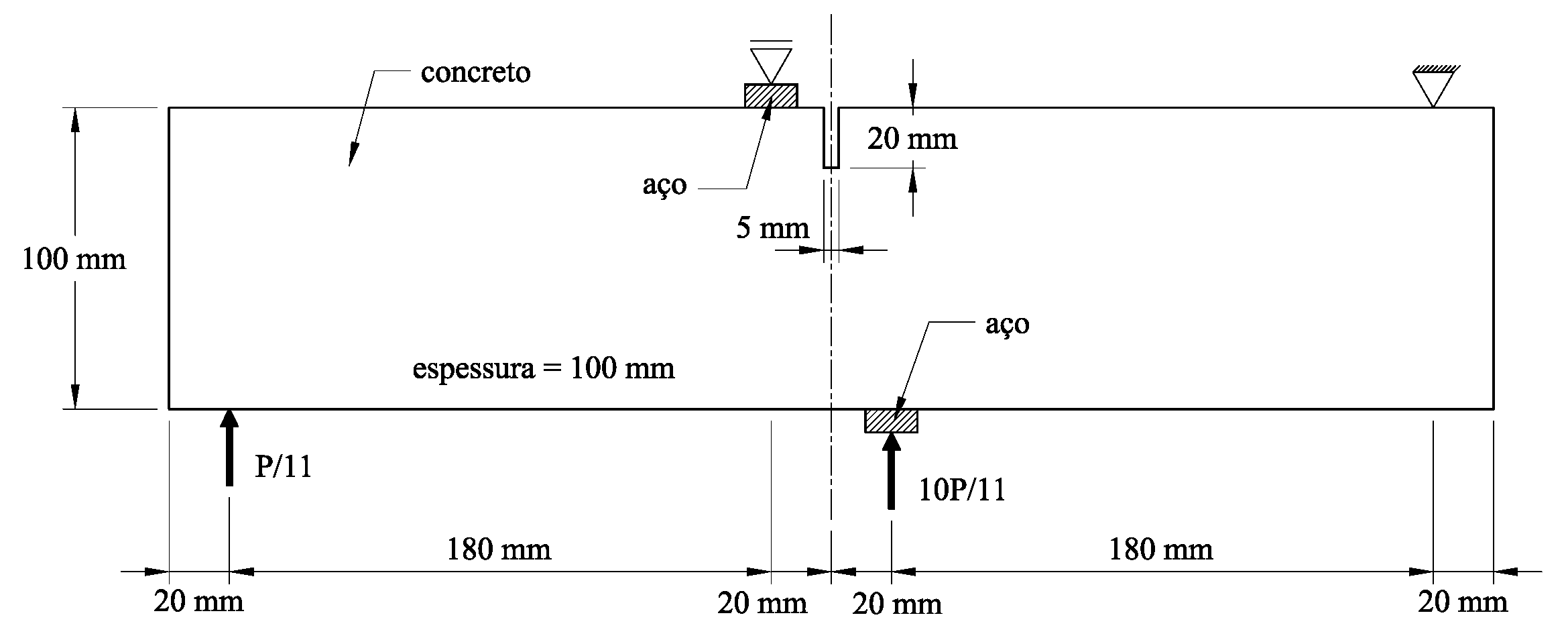
Aqui se usa o INSANE para a descrição do comportamento do concreto sujeito a uma fissura coesiva a partir do ensaio de cisalhamento em 4 pontos proposto por Wells e Sluys (2001) – Figura 1.  A discretização adota uma malha de elementos finitos triangulares de seis nós em estado plano de tensão – Figura 2. A simulação numérica assume os seguintes parâmetros para o concreto: E = 3.5 × 10⁴ N⁄mm², ν = 0.2, f_t = 3.0 N⁄mm², G_f = 0.1 N⁄mm, d_init = 1.0 N⁄mm (rigidez ao cisalhamento constante). Para as placas de carga foram adotados os valores do aço com E = 2.1 × 10⁵ N⁄mm² e ν = 0.3. Para a carga concentrada mostrada na Figura 1 adota-se o valor de P = 1.0 N. O método de controle do ensaio foi o controle do deslocamento vertical do nó 2419 (ver Figura 2). Os detalhes do modelo físico adotado, dos conceitos do G/XFEM e das técnicas de implementação computacional podem ser vistos na dissertação de mestrado de Wolff (2010). O caminho de propagação da fissura resultante pode ser visto na Figura 3. A Figura 4 mostra a deformada da malha ao final do ensaio numérico. A curva de fator de carga versus deslocamento vertical do nó 66 (ver Figura 2) está descrita na Figura 5. Nessa curva, verifica-se o comportamento de softening ou amolecimento (tendência de decréscimo após o pico da curva). Esse comportamento é característico para esse tipo de análise fisicamente não linear, adotada aqui para o concreto. Adicionalmente, a Figura 6 mostra o campo de deslocamentos da viga na direção x. Nessa figura fica evidente a capacidade do modelo numérico de descrever o salto no campo de deslocamentos provocado pela presença da fissura.

Figura 1 – Geometria e condições de contorno

Figura 2 – Malha formada por 1206 elementos triangulares de seis nós

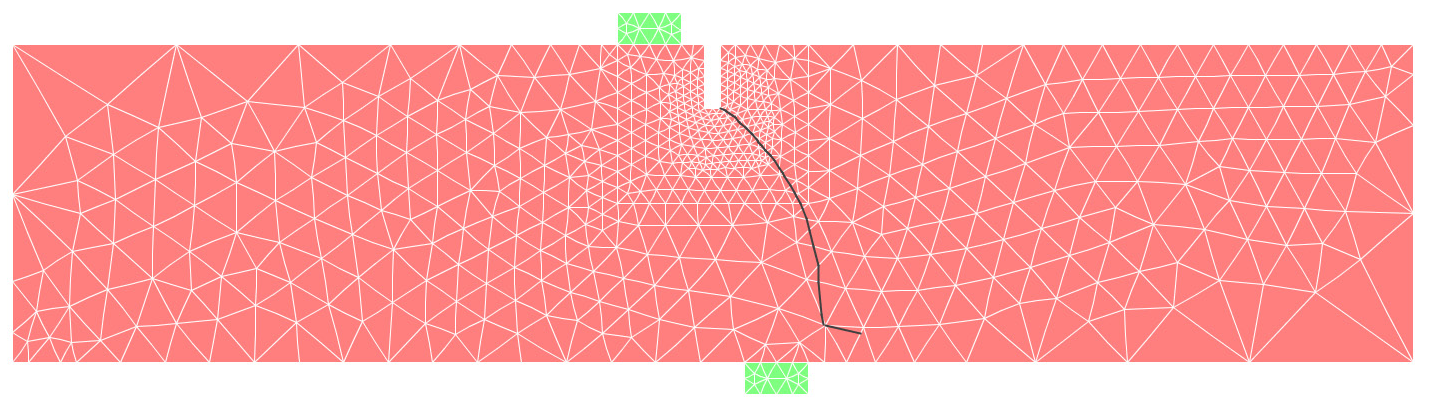
Figura 3 – Propagação da fissura coesiva

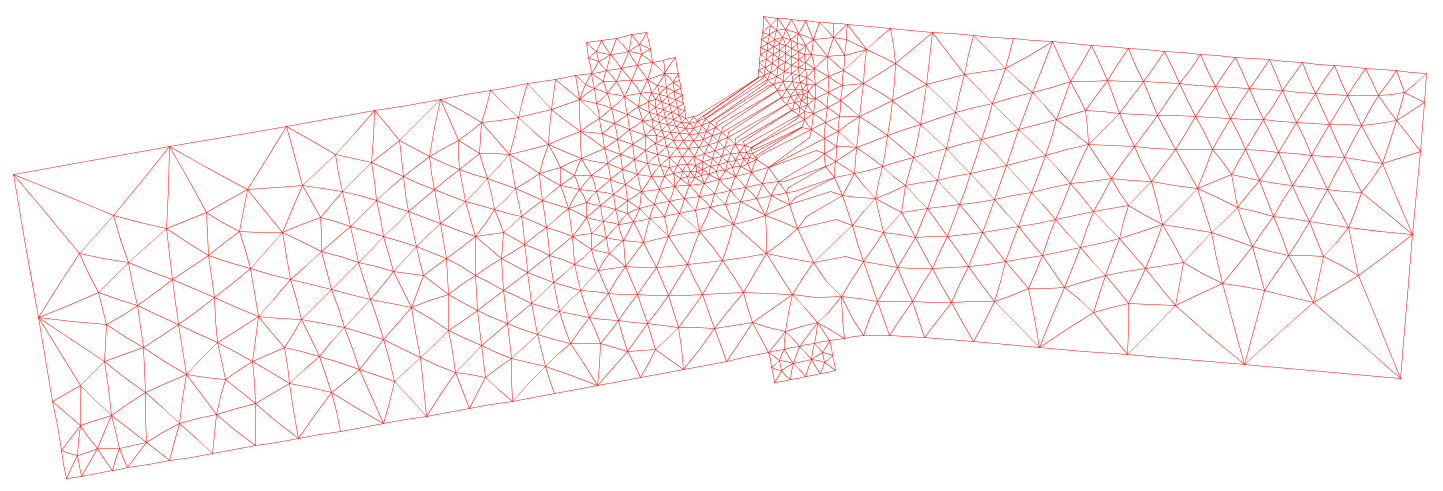
Figura 4 – Deformada da malha

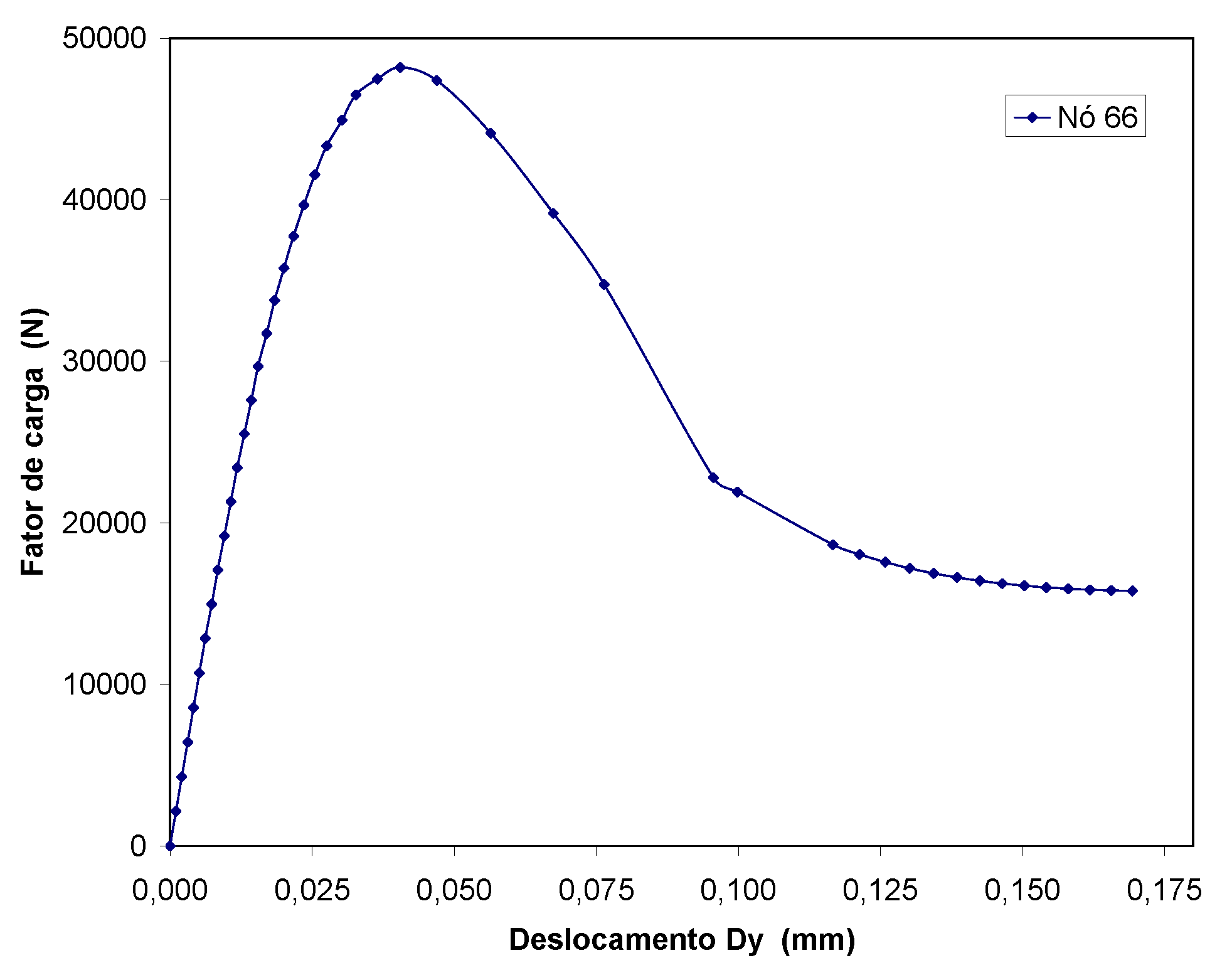
Figura 5 – Curva do fator de carga x deslocamento vertical do nó 66 (ver Figura 2)

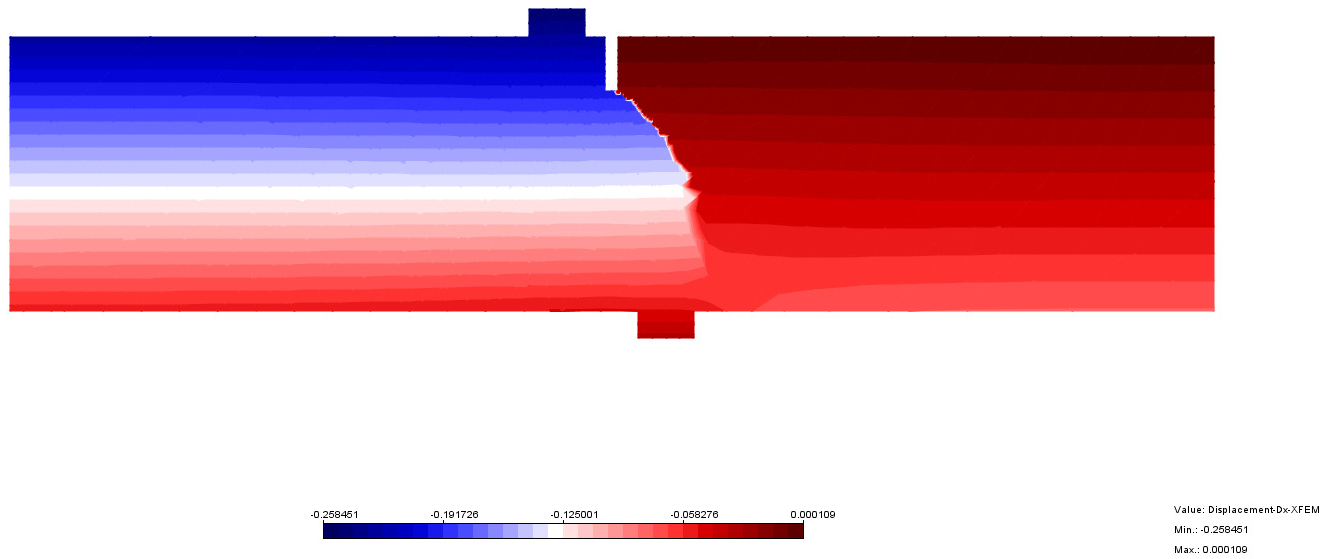
Figura 6 – Salto no campo de deslocamentos na direção x

Referências

• Wells, G. N. e Sluys, L. J., 2001. ‘A new method for modelling cohesive cracks using finite elements’. International Journal for Numerical Methods in Engineering, vol. 50(12), pp. 2667-2682.
• Wolff, K. P., 2010. Implementação computacional de um modelo de fissuração para o concreto baseado no método dos elementos finitos estendido (XFEM). Dissertação de mestrado, Universidade Federal de Minas Gerais, Belo Horizonte, MG, Brasil.