Thin plate model – Reissner-Mindlin plate

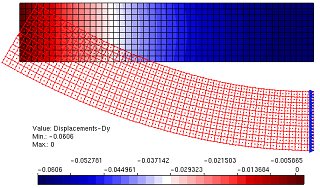
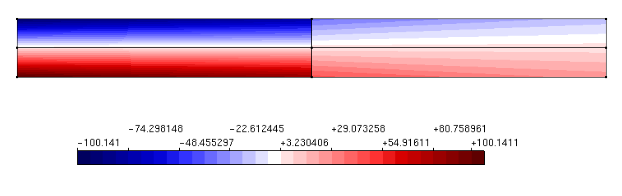
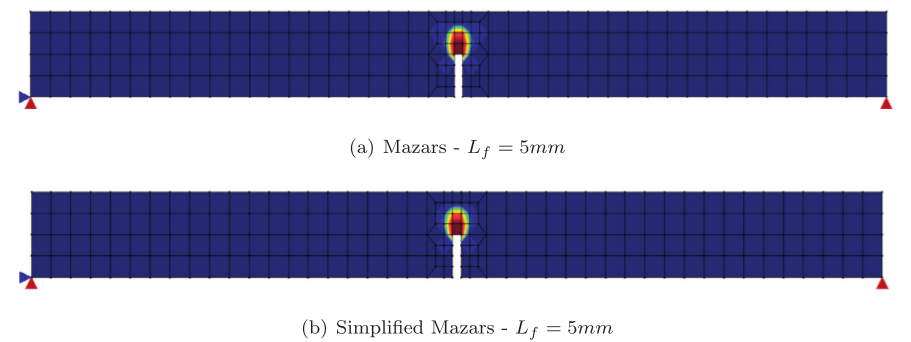
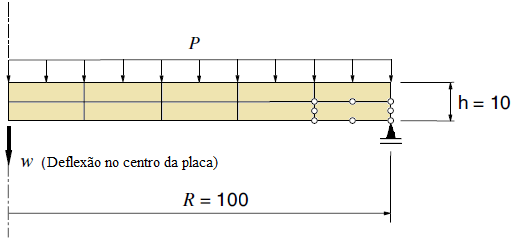
A circular plate with a circular hole at the center under a uniformly distributed load along the inner edge and simply supported along the outer edge (Figure 1) was modeled in the INSANE to compare the displacements obtained with the analytical solution proposed by Timoshenko and Woinowsky-Krieger (1959). In this simulation was used the quadrilateral element with four nodes (Q4). As Reissner-Mindlin’s theory was used to analyze a thin plate, it was necessary to use two anti-block techniques implemented by Saliba (2007). The same model was analyzed twice – once using the selective integration technique (IS) and other time the assumed transverse shear strain field technique (CI) was used. Due the double symmetry in the plate, only ¼ of the plate was used according to Figure 2. The Figure 3 presents a comparative of the vertical displacements along the line of symmetry collinear to the x-axis between the analytical solution and the results obtained by IS and CI techniques (see Figure 4).

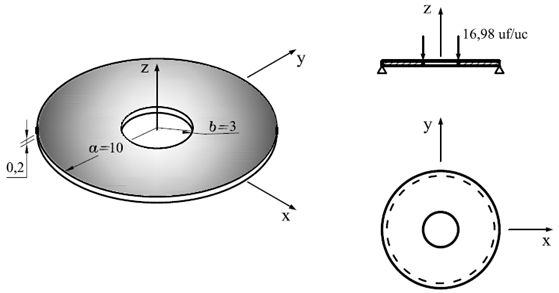
Figure 1 – Geometry, load and boundary conditions

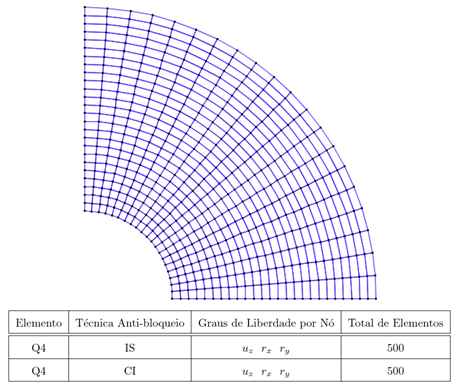
Figure 2 – Finite elements model

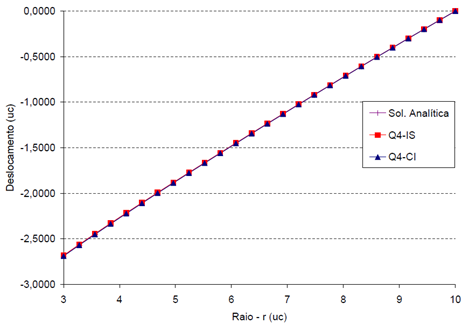
Figure 3 – Vertical displacements

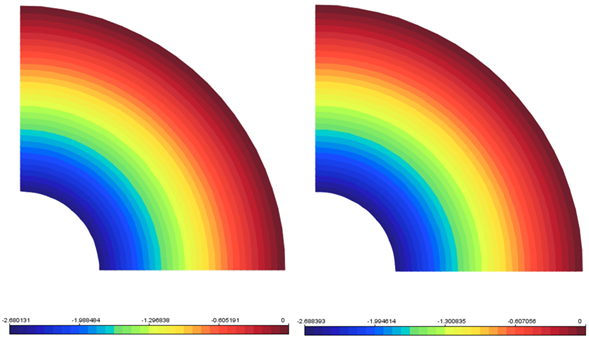
Figure 4 – Vertical displacements
(a) Selective integration (IS)
(b) Assumed transverse shear strain field (CI)

References

• Timoshenko, S. e Woinowsky-Krieger, S., 1959. ‘Theory of Plates and Shells’. McGraw-Hill, Nova York.
• Saliba, S. S., 2007. Implementação computacional e análise crítica de elementos finitos de placas. Master thesis. Universidade Federal de Minas Gerais (UFMG), Brazil.