Plasticity models

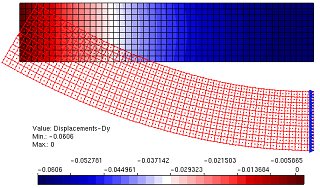
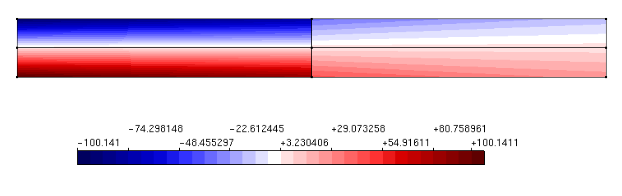
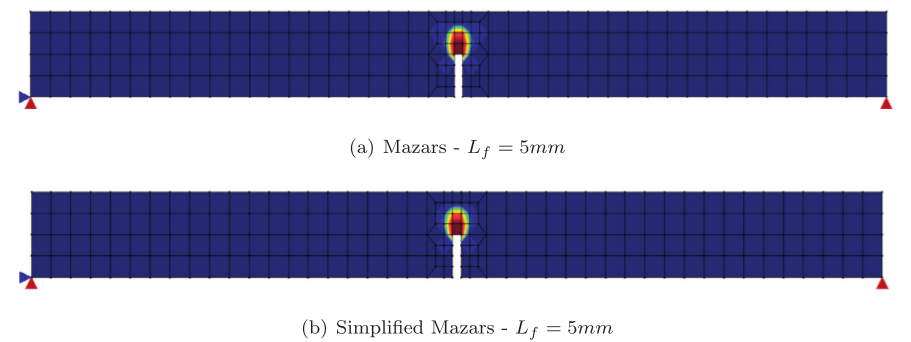
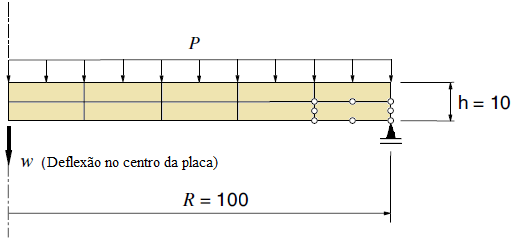
The INSANE system has been used to simulate a circular plate simply supported and subjected to uniformly distributed loading. The geometric characteristics and finite elements adopted are shown in Figure 1. The plate is discretized into ten quadrilateral axissimetric elements of nodes, which are distributed in two layers along the thickness. In order to determine the load limit for the plate by numerical analysis, a perfectly plastic model with the von Mises and Tresca flow criteria was adopted, formulated according to the Theoretical-Computational Environment developed in Penna (2011) and implemented in the master’s thesis of Oliveira (2016). The diagram of Figure 2 represents an equilibrium trajectory “Central deflection x Distributed load intensity”. Figure 3 illustrate the values for the plastic flow variable accumulated along the equilibrium trajectory for the solution obtained by Souza Neto et al. (2008) – Figure 3-a and for the models of Tresca Figure 3-b and von Mises Figure 3-c in different phases of loading. The results agree with the numerical results obtained by Souza Neto et al. (2008).

Figure 1 – Geometry and finite elements mesh. Adapted from Souza Neto et al. (2008)

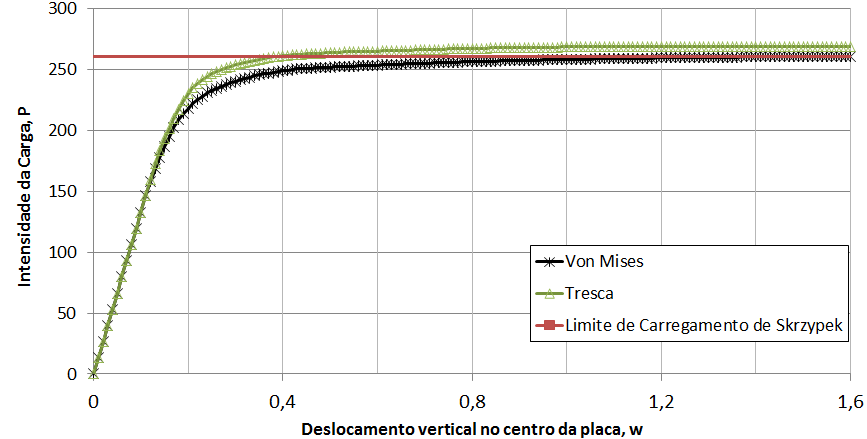
Figure 2 – Load x deflection

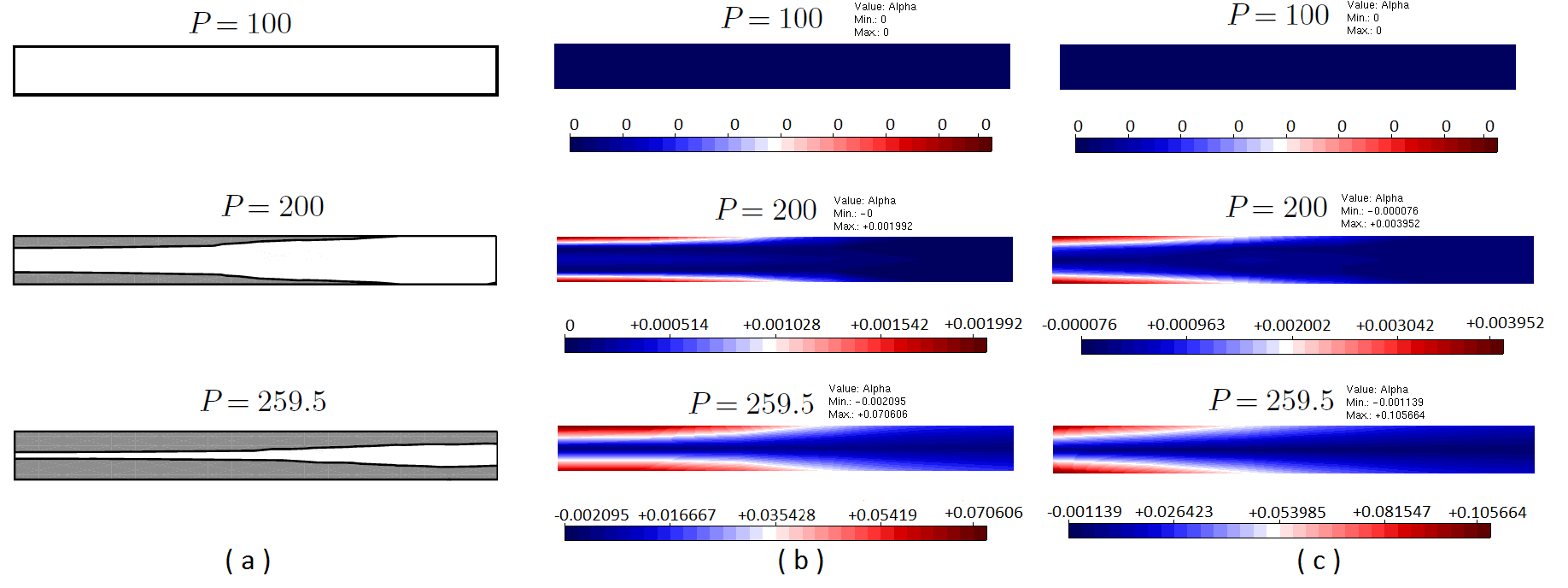
Figure 3 – Evolution of plastic flow

References

• Oliveira, D. B., 2016. Implementação computacional de modelos elastoplásticos para análise fisicamente não linear. Master thesis. Universidade Federal de Minas Gerais (UFMG), Brazil.
• Penna, S. S., 2011. Formulação multipotencial para modelos de degradação elástica: Unificação teórica, proposta de novo modelo, implementação computacional e modelagem de estruturas de concreto. Doctoral dissertation, Universidade Federal de Minas Gerais, Belo Horizonte, MG, Brazil.
• Skrzypek, J. J., 1993. Plasticity and Creep Theory. CRC Press, Londres.
• Souza Neto, E. A., Peric, D. e Owen, D. R. J., 2008. Computational Methods for plasticity: Theory and application. Wiley, Swansea, EUA.